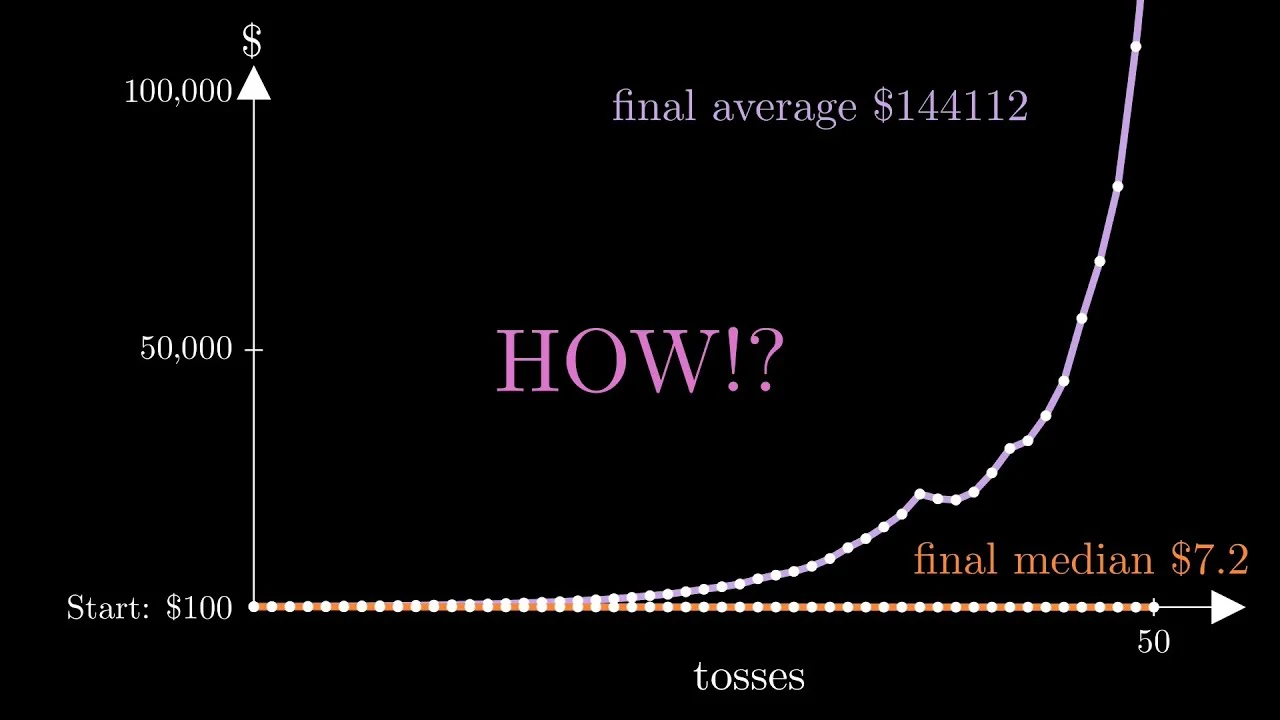
How is this video calculating that a 50% chance of 80% gain and a 50% chance of 50% loss yields a positive expected gain? An alternating string of heads and tails will drive your money to zero - a 50% loss (1/2) would be balanced by a 100% gain (2/1) in a fair system.
This is true if you’re betting everything you have. By not having shrinking bets after losses you can tap into the net gains. Compare 1 win followed by 1 loss with $100 start:
Win is $100+$80 = $180
Loss is $180-$90 = $90
Compare with fixed bets of $50 with bank of $100:
Win is $100+$40 = $140
Loss is $140-$25 = $115
Because if you gamble in small increments the odds are in your favor. If you gamble your entire wealth then you’ll likely lose.
Lets say you’re gambling in $5 increments. The odds are 50/50, if you lose then you’ll have $2.5, and if you win you’ll have $9. That’s a 50% chance to lose $2.5 and a 50% chance to gain $4, the actual risk is if you lose too many times in a row that you don’t have enough money to gamble with. Otherwise, you’ll slowly gain money.
Ah, I was assuming that the premise was all-in on each gamble. It’s true that it will work with small increment gambles.
The guy in the video did his math wrong.
And 80% gain gives you 1.8x. A 50% gain gives you 0.5x. When combining them, you multiply them, giving you 0.9x, which is a 10% loss with each set of 2 flips.
Try it yourself: $100 x 1.8 = $180. $180 x 0.5 = $90. So you start with $100 and end with $90.
What the fuck? 50% gain gives you 1.5x not 0.5x For 50% decrease, you multiply by 0.5
Whoops, typo.
What is wrong with it? That’s exactly what he shows in the video. When betting it all, equal wins and losses is a net loss. The point is betting some fraction such that the gains overtake the losses
Here is an alternative Piped link(s):
http://piped.video/watch?v=_FuuYSM7yOo
Piped is a privacy-respecting open-source alternative frontend to YouTube.
I’m open-source; check me out at GitHub.
It’s basically an equation to calculate the “sweet spot” of how much you should spend in gambling in order to get the best returns. If you gamble too much, you lose too much when you fail. If you gamble too little, you earn too little to make enough back. I don’t know how this applies to investing but it’s well known in gambling, which is why casinos always have the odds against you so that you’re still more likely to lose or have a minimum bet that’s way higher than the optimal bet.
So its more like a slightly lucrative “if you like to play moderate-stakes poker with your buddies poker league” or something or investing context?
deleted by creator
deleted by creator
Make smaller bets that are more likely to win and that have smaller risks of downside for a higher “guranteed” positive return rate. —Me (my understanding)
Is this an accurate understanding? Like focus on additive gain rather than trying to “hit the motherlode” or something?
Sorry, I didn’t feel like he really spelled out a takeaway means of immediately understanding and applying this
The key is not letting your losses affect your bet amount. With the gain being only 80% instead of 100%, betting your bank means 1 win and 1 loss leaves you with less than you started. Making your bet amount fixed between flips means 1:1 will instead give you a net gain. The Kelly Criterion says there is an optimal proportion of bank you can bet that will maximize this gain over many flips
Is there a metaphysical or like everyday life kind of application to this, everybody seems to be talking about Gambling or like using that metaphor at the very least. I don’t gamble (in name if not in deed) but I sense there’s a takeaway I can sort of apply to life buried in here. Any thoughts?
My takeaways would be:
- Never trust averages on their face
- Being consistent gives you an advantage
- Always be looking to reevaluate your situation and maximize what you can get out of it
Should we basically do the life equivalent of “invest in VGRO” index funds and focus always on the smaller more time-tested actions that lead to improvement incrementally but meaningfully/steadily?