Do I understand the physical and philosophical ramifications of quantum physics? No.
Do I understand the mathematical machinery of quantum physics and how to do calculations for quantum systems? Also no, but I’m working on it.
I bet no one truly understands the mathematical machineries, Renormalization is hell of a drug.
Renormalization
Whoa there! I bet you don’t even know anymore how many things you have to not understand before you can fail to understand renormalization.
Anyway, when normal people talk about quantum physics, they aren’t talking about that.
For the first question, I would recommend reading the philosopher and physicist Francois-Igor Pris who not only seems to understand the deep philosophical origins of the problem, but also provides probably the simplest solution to it. Pris points out that we cannot treat the philosophical ramification in isolation, as if the difficulty in understanding quantum physics originates from quantum physics itself. It must originate from a framework in which we are trying to apply to quantum physics that just breaks down, and therefore it must originate from preconceived philosophical notions people have before even learning of quantum physics.
In other words, you have to go back to the drawing board, question very foundational philosophical notions. He believes that it originates from the belief in metaphysical realism in the traditional sense, which is the idea that there is an objective reality but it is purely metaphysical, i.e. entirely invisible because what we perceive is merely an illusion created by the conscious mind, but somehow it is given rise to by equivalent objects that are impossible to see. For example, if you have a concept of a rock in your mind, that concept “reflects” a rock that is impossible to see, what Kant had called the thing-in-itself. How can a reality that is impossible to observe ever “give rise to” what we observe? This is basically the mind-body problem.
Most academics refuse to put forward a coherent answer to this, and in a Newtonian framework it can be ignored. This problem resurfaces in quantum physics, because you have the same kind of problem yet again. What is a measurement if not an observation, and what is an observation if not an experience? You have a whole world of invisible waves floating around in Hilbert space that suddenly transform themselves into something we can observe (i.e. experience) the moment we attempt to look at them, i.e. they transform themselves suddenly into observable particles in spacetime the moment we look.
His point is ultimately that, because people push off coming up with a philosophical solution to the mind-body problem, when it resurfaces as the measurement problem, people have no idea how to even approach it. However, he also points out that any approach you do take ultimately parallels whatever solution you would take to the mind-body problem.
For example, eliminative materialists say the visible world does not actually exist but only the nonvisible world and that our belief we can experience things is an illusion. This parallels the Many Worlds Interpretation which gets rid of physical particles and thus gets rid of all observables and only has waves evolving in Hilbert space without observables. Idealists argue in favor of getting rid of invisible reality and just speak of the mind, which if you read the philosophical literature you will indeed find a lot of academics who are idealists who try to justify it with quantum mechanics.
Both of these positions are, in my view, problematic, and I like Pris’ his own solution based on Jocelyn Benoist’s philosophy of contextual realism which is in turn based off of Ludwig Wittgenstein’s writings. Benoist has written extensively against all the arguments claiming that reality is invisible and has instead argued that what we experience is objective reality as it is exists independent of the observer but dependent upon the context of the observation. Thus he is critical of pretty much all of modern philosophers who overwhelmingly adhere either to metaphysical realism or to idealism. There is no mind-body problem under this framework because reality was never invisible to begin with, so there is no “explanatory gap.”
Apply this thinking to quantum mechanics then it also provides a solution to the measurement problem that is probably the simplest and most intuitive and is very similar to Carlo Rovelli’s interpretation. Reality depends upon context all the way down, meaning that the properties of systems must be context variant. And that’s really the end of the story, no spooky action at a distance, no multiverse, no particles in two places at once, no language of observer-dependence, etc.
Whenever you describe physical reality, you have to pick a coordinate system as reality depends upon context and is not “absolute,” or as Rovelli would say, reality depends upon the relations of a system to every other system. Hence, if you want to describe a system, you have to pick a coordinate system under which it will be “observed,” kind of like a reference frame, but the object you choose as the basis of the coordinate system has to actually interact with the other object. The wave function then is just a way for accounting for the system’s context as it incorporates the relations between the system being used as the basis of the reference frame and the object that it will interact with.
Basically, it is not much different from Copenhagen, except “observer-dependence” is replaced by “context-dependence” as the properties of systems are context variant and any physical system, even a rock, can be used as the basis of the coordinate system. But, of course, if you want to predict what you will observe, then you always implicitly use your own context as the basis of the coordinate system. This is a realist stance, but not a metaphysical realist stance, because the states of particles are not absolute, there is no thing-in-itself, and the reality is precisely what you perceive and not some waves in Hilbert space beyond it (these are instead treated as tools for predicting what the value will be when you measure it, and not itself an entity). Although, it is only whether or not they have a property at all that is context variant.
If two observers have interacted with the same particle, they will agree as to its state, as you do not get disagreements of the actual values of those particles, only whether or not they have a state at all. They would not be verbal disagreements either, because if an observer measures the state of a particle then goes and tells it to someone else, then it also indirectly enters their context as they would become correlated with that particle through their friend. You only get disagreements if there is no contact. For example, Wigner’s friend paradox, where his friend has measured the particle but has not told him the results nor has he measured it himself, from his context it would indeed have no state.
The “collapse” would then not be a collapse of a physical “wave” but, again, reality is context variant, and so if you interact with a system, then it changes your relation to it, so you have to update the wave function to account for a change in context, kind of like if you change your reference frame in Galilean relativity. Everything is interpreted through this lens whereby nature is treated as context variant in this way, and it resolves all the paradoxes without introducing anything else. So if you can accept that one premise then everything else is explained. By abandoning metaphysical realism, it also simultaneously solves the other philosophical problems that originate from that point of view, i.e. the “hard problem” does not even make sense in a contextual realist framework and is not applicable.
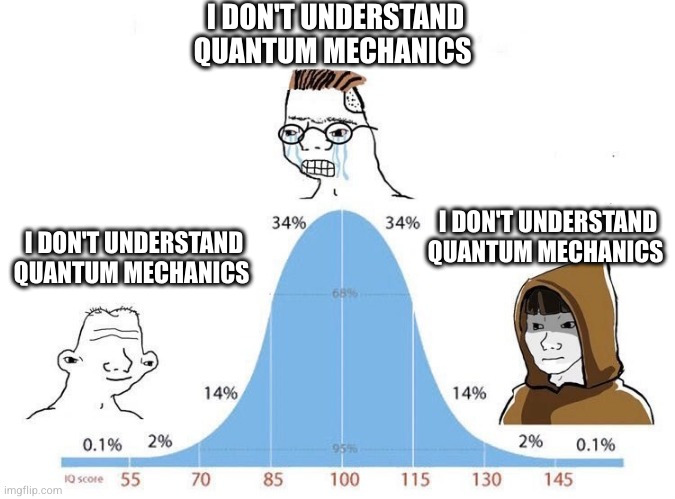
This implies the majority of people believe they understand quantum mechanics, which I’m sure is not true. In reality, the overwhelming majority of people would say they don’t understand quantum physics.
Bell curve is the wrong meme format for what you’re trying to convey
I misread and thought top guy was also saying he didn’t understand quantum physics, and thought it was a way better meme than it was.
Make it and post it!
Probably the bell curve of physics students, and not just of all people on Earth.
- It’s a meme. Memes change meaning over time and can detach from the original/ literal meaning.
- Even when taken literal, you don’t know the group of people in the plot. It’s obviously not every single person on earth since where are those who don’t even know about quantum physics. It might include students, interested lay people, … It’s bad science not to include that but it’s against just a meme. You don’t even know the y axis. It might be confidence and not the number of people
This meme is bullshit.
Thanks for clarification!
Yes, there are a lot of intuitive understandings in the literature if you’re willing to look for it. The problem is that most people believe in a Newtonian view of the world which just is not compatible with quantum physics, so it requires you to alter some philosophical beliefs, and physics professors don’t really want to get into philosophical arguments, so it’s not really possible to reach a consensus on the question in physics departments. Even worse, there’s rarely a consensus on anything if you go to the philosophy department. So it’s not really that there are not very simple and intuitive ways to understand quantum mechanics, it’s that it’s not possible to get people to agree upon a way to interpret it, so there is a mentality to just avoid interpretation at all so that students don’t get distracted from actually understanding the math.
Yeah maybe shift the X scale by 40 IQ points and it would be more accurate.
FTFY
You should upload this as a post!
I’m often reminded of a cartoon I saw years ago, with a stereotypical Einsteinish physicist standing in front of a chalkboard, looking at this enormously complex formula with a big blank space in the middle of it. Then he gets a “eureka” expression and starts writing in the blank space. Then he steps back, and you can see that he’s filled the blank space with “and then something happens”.
Me neither but I’m on the left side
Im lost but at least i know how fast i am.
c it’s not that hard.
For me, a hurdle to get over was trying to understand in the context of my experience of the world. Like, popsci has this whole “is X a wave or a particle? Scientists still don’t know…” schtick. And our understanding at some level is, “here’s the math to describe this system.”
Getting away from always mapping that onto the world we experience is, IMHO, really important. Not that it should be understood solely as math, by any means! But you really need to throw away intuition gained from the macroscopic world we interact with.
My favorite example was looking at reflection coefficients and seeing that an “infinite wall” is the same as an “infinite cliff” — you’ll reflect off of both. Which makes zero sense if you imagine driving a bumper car into a wall (bounce back) vs. over an infinite cliff! But it does me make sense in its own way, and after building up intuition, so do other “weird” and counterintuitive things.
Waves are underrated in pop-sci context. Even classical waves you can make with household items like strings can have counterintuitive and cool behaviors!
Absolutely. As a kid I liked to see how many nodes I could get into ‘simple’ system of rotating a jump rope tied to something fixed at one end. I can’t say my understanding of harmonics is great now, but I can at least relate it to personal experience.
Understanding classical waves better is what helped me wrap my mind around the physical meaning of the uncertainty principle. It’s not a technical limitation, and it’s not just because you need to interact with something to measure it. It’s just a property of waves. Since small enough particles exhibit the properties of waves, it only makes sense that we can’t know their location and momentum at the same time with arbitrary precision.
The velocity of a wave is a function of its frequency and wavelength. But imagine a highly localized wave, essentially just a peak. What’s its frequency? Well, we find that it doesn’t have one frequency! If you decompose the wave, you find its mathematically a superposition of multiple sine or cosine functions with different frequencies and therefore velocities. So the more localized the wave is, i.e the more you know its position, the less and less you know about its frequency and therefore velocity.
This stuff blew my mind when it was first explained to me.
einstein had problems with it. don’t feel bad.
deleted by creator
haha quantum loop gravity haha