Is the curve less direct or like meandering?
Which is more “gradual” or smooth?
Are you asking how do 2 lines pass through the same point? Try it out with a paper and pencil.
They only need to overlap at the start and end, meaning the rest of the line can be way off and it’ll still start and stop at the same places. Here’s a quick graph courtesy of WolframAlpha showing three curves with the same start and end point.
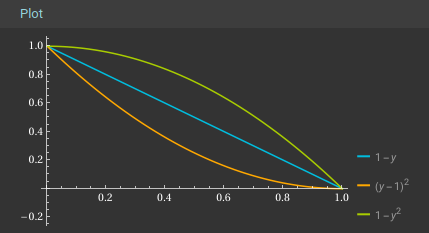
Which line is more gradual or smooth really depends on what you mean by those terms.
Another way to visualise it is to imagine a string tied taut between two posts making a straight line. If you add some slack to the string so it’s no longer taut you’ll see the middle curve as it’s pulled down by gravity, but it’s still tied to the same two posts so it starts and ends in the same place as the taut one.
Are you talking about an asymptote? Things “in the limit” is maths voodoo whenever infinity is involved
That’s a big part of road design.
According to Ars Magicka rules, I’d say Rego+Vim
Curved slopes can be defined as any combination of mathematical formulas on a graph. This means there are any combination of ways to get feom one point to another - effectively infinite.
For a 2-dimenzional plane, these curves are usually defined as a value (y, vertical axis) that is calculated at each location of another value (x, horizontal axis).
A linear slope or “straight line” is a simple rise over run. For every x units you travel in a direction, your height will change y units. On a 2d plane it is the “most” distance efficient way to get from A to B.
How you define “smoothness” matters… In math land, the linear slope is the smoothest as its curvature never changes. In real life it results in an abrupt stop and start at either end with a constant velocity along the line.
A real life “smoothest path” when changing the Y-value/height of your line involves a cubic or logarithmic slope-in and slope-out of the line, like this bezier curve.. Think of the “steepness” as the speed of your car (how fast your distance changes along the y axis), and the x axis the time you have been driving. Gradually pushing the accelerator on your car until you’re up to speed, coasting in the middle, then gradually apply the brakes until you come to a stop at point 2.



